Análise exploratória de dados – parte I

* Texto livremente adaptado do tutorial publicado por Andrew Andrade no Data Science Guide e traduzido pela editora/analista de dados Bruna Baldini, com revisão e comentários da Escola de Dados em colchetes.

Análise exploratória de dados (AED) é uma etapa muito importante que se realiza depois da engenharia de características [feature engineering, ou seja, o pré-processamento dos dados para técnicas de machine learning, aprendizado de máquinas] e da coleta de dados. Deve-se colocá-la em prática antes de qualquer tipo de modelagem em si. Isso acontece pois é essencial que o cientista de dados seja capaz de entender a natureza dos dados sem fazer suposições.

O objetivo da AED é utilizar síntese estatística e técnicas de visualização para entender melhor os dados e identificar insights sobre tendências e a qualidade dos dados, bem como para formular hipóteses e fazer suposições nas análises. Análise exploratória de dados NÃO SE TRATA de elaborar visualizações sofisticadas ou mesmo esteticamente agradáveis. O objetivo é fazer testes e encontrar respostas com os dados. Seu objetivo, enquanto cientista de dados, deveria ser criar um gráfico, no qual qualquer um que o olhasse por alguns segundos pudesse entender o que se passa. Caso contrário, a visualização é muito complicada (ou sofisticada) e algum similar simplificado deveria ser utilizado.

AED é também uma prática muito iterativa, já que inicialmente fazemos suposições com base nas primeiras visualizações exploratórias, imediatamente construímos alguns modelos. De modo que, ao mesmo tempo que construímos visualizações dos resultados do modelo, incrementamos estes modelos.

Antes que possamos começar os estudos sobre exploração de dados, vamos primeiro aprender diferentes tipos de dados ou níveis de mensuração. Eu recomendo fortemente que você leia Levels of Measurement no “online stats book”, e continue a ler as seções para aprimorar os seus conhecimentos com estatística. Esta seção é apenas um resumo.

Os dados aparecem sob vários formatos, entretanto podem ser classificados em dois principais grupos: estruturados e não estruturados.

Dados estruturados são aqueles que apresentam altos níveis de organização intrínseca, por exemplo em termos numéricos ou categóricos. Temperatura, número de telefone e gênero são exemplos de dados estruturados.

Dados não estruturados são aqueles que não têm uma organização estruturada usual. Exemplos de dados não estruturados são: fotos, imagens, áudios, linguagens de texto, entre muitos outros. Há um campo emergente chamado Deep Learning que utiliza um conjunto de algoritmos que tem um bom desempenho com dados não estruturados. Neste guia serão destacados os dados estruturados; contudo forneceremos informações pontuais sobre alguns tópicos relevantes em Deep Learning.

Os dois tipos mais comuns de dados estruturados usualmente tratados são variáveis categóricas (que têm um conjunto finito de valores) ou valores numéricos (que são contínuos).

Variáveis categóricas

[Com base no artigo Levels of Measurement, agora, será abordado quatro tipos de escalas utilizadas em variáveis: nominais, ordinais, numéricas com escala intervalar e numéricas com escala de razão.]

Variáveis categóricas podem ser também nominais ou ordinais. 

Dados nominais não têm ordenação intrínseca nas categorias. Por exemplo: gênero (masculino, feminino, outros) não tem uma ordenação específica. 

Dados ordinais têm uma ordenação explícita, por exemplo os 3 níveis de uma máquina de lavar (alto, médio e baixo). Uma tabela de frequência (contagem de cada categoria) é a estatística mais comum usada para descrever dados categóricos de cada variável, e o gráfico de barras ou gráfico waffle (apresentado a seguir) são duas possibilidades que podem ser utilizadas.

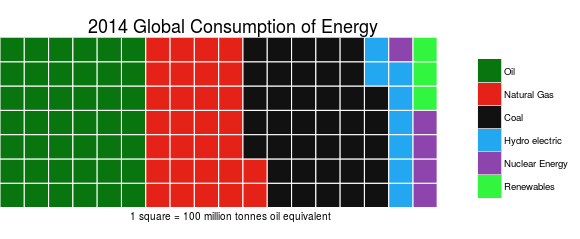
Consumo global de energia em 2014: 1 quadrado = equivale a 100 milhões de toneladas de petróleo. Verde esc. – petróleo; Verm. – gás natural; Preto – carvão; Azul – hidrelétrica; Roxo – energia nuclear; Verde cl. – renováveis

Ainda que o gráfico de pizza se constitua como uma forma muito comum para representar variáveis categóricas, ele não é muito recomendado pois as pessoas têm dificuldade para interpretar proporções retratadas com ângulos. Explicado de maneira bem simples pelo professor de estatística e visualização, Edward Tufte: “Gráficos de pizza são ruins”. Outros concordam e até mesmo dizem: “Os gráficos de pizza são os piores”.

Por exemplo: o que você conclui a partir dos seguintes gráficos de pizza? 

(As imagens foram retiradas do artigo ‘Pie Charts Are the Worst’)

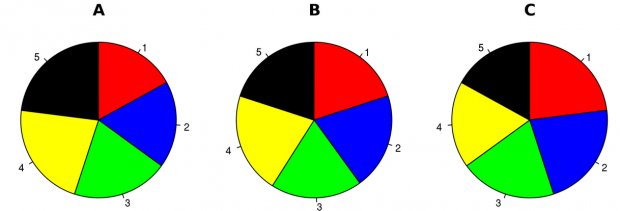
Os gráficos parecem idênticos, e leva algum tempo para entender os dados. Agora, compare-os com os correspondentes em gráficos de barra:

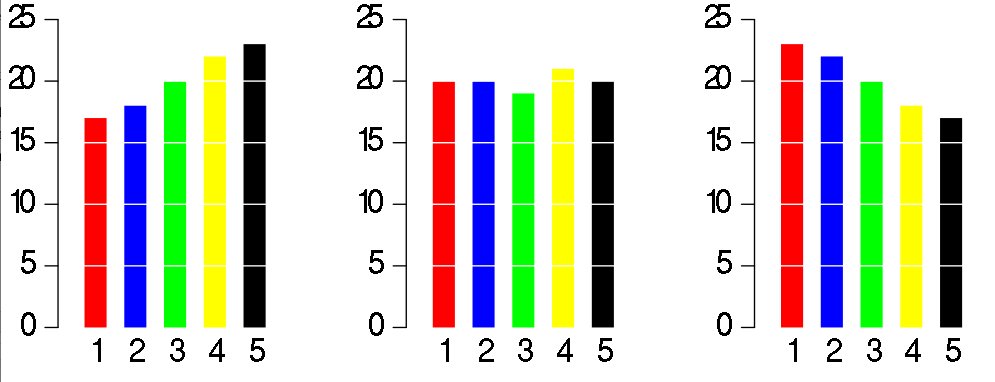
O leitor compara instantaneamente 5 variáveis. Já que a maioria das pessoas têm dificuldade em comparar ângulos, são recomendados gráfico de barras ou gráficos waffle. Há muitas outras visualizações que não são recomendadas: gráfico de radar/teia de aranha, gráficos de barras ou colunas empilhadas e muitos outros gráficos com excesso de informação apresentada simultaneamente.

Por exemplo, esta visualização é muito complicada e difícil de se entender:

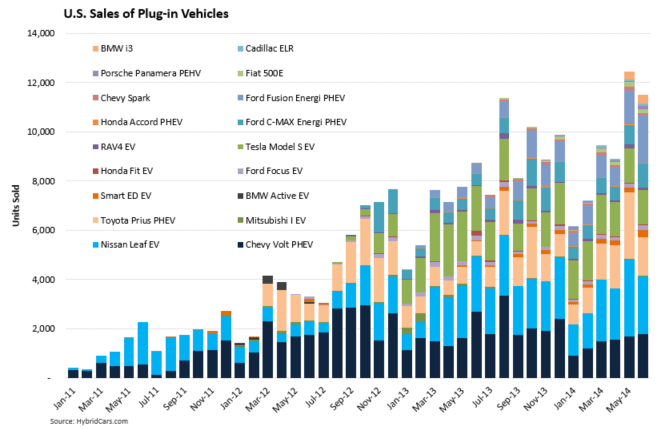
Frequentemente menos é mais: o plot redux como um simples gráfico de linha. 

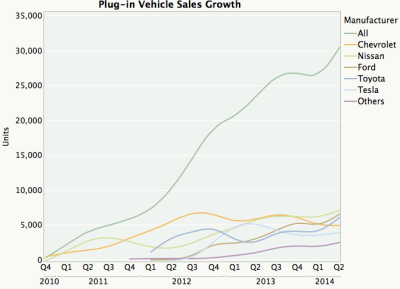
Índice de crescimento de vendas dos veículos

Ao tratar dados multi-categóricos, evite usar gráficos de barras ou colunas empilhadas. Siga os manuais escritos por Solomon Messing (cientista de dados que conheci enquanto trabalhava no Facebook).

Variáveis numéricas

Variáveis numéricas ou contínuas podem assumir qualquer valor dentro de um intervalo finito ou infinito. Exemplos: temperatura, peso e largura. Há dois tipos de variáveis numérica: aquelas de intervalos e as de razão. Variáveis de intervalo têm escalas numéricas e a mesma interpretação ao longo de toda a escala, mas não têm de forma alguma um zero absoluto [ou seja, o que se considera “zero” é um valor arbitrário, que não representa a ausência absoluta do fenômeno mensurado e, portanto, estas escalas admitem valores negativos]. Por exemplo, faz sentido subtrair ou adicionar temperatura em Fahrenheit ou Celsius (a diferença entre 10 e 20 graus é a mesma diferença que 40 para 50 graus), mas a temperatura não pode ser multiplicada [Como nota o onlinestatbook: o grau zero em Fahrenheit não significa a ausência de temperatura, ou seja, de qualquer energia molecular cinética]. 

Outro exemplo: um dia em que estiver duas vezes mais quente que outro pode não ter o dobro da temperatura [Isto pois, nestes casos, o cálculo de razões matemáticas depende de qual ponto é (arbitrariamente) considerado o zero. Não há sentido em dizer que a razão entre 2 grau celsius e 4 graus celsius é a mesma razão entre 20 graus e 40 graus].  

[O outro tipo de variável numérica abordada é aquela com escalas de razão.] “A medida de escala de razão é a escala mais informativa. É uma escala [ou variável] de intervalo com a propriedade adicional de que sua posição  zero indica a ausência da quantidade medida. Você pode pensar em uma escala de razão como as três escalas anteriores [nominal, ordinal e intervalar] compactadas em apenas uma. Da mesma forma que uma escala nominal, a escala de índice fornece um nome ou uma categoria para cada objeto (os números servem como identificadores). Como uma escala ordinal, os objetos são ordenados (ordenação numérica). Como uma escala de intervalo, a mesma diferença em dois lugares na escala tem o mesmo significado. E, além disso, a mesma razão entre duas posições na escala também tem o mesmo significado.” [citação do onlinestatsbook] Um bom exemplo de uma escala de razão é largura, desde que tenha um zero real e possa a ser adicionado, subtraído, multiplicado ou dividido.  

Categorização (Numérico para Categórico)

Categorização, também conhecida como discretização, é o processo de transformar variáveis numéricas em categóricas. Por exemplo: idades podem ser categorizadas em 0-12 (criança) 13-19 (adolescente), 20-65 (adulto), 65 + (melhor idade). A categorização é eficaz quando usada como um filtro para reduzir falhas ou a não linearidade; alguns algoritmos, como as árvores de decisão, requerem dados categóricos. Técnicas de categorização incluem usar parâmetros iguais (com base no intervalo), igual frequência em cada categoria, rankings variados, quantis ou funções matemáticas (como o log [logaritmo]). Categorização pode ainda ser usada com base em informação de entropia ou ganho de informação [A respeito de técnicas de categorização, vale conferir este tutorial, em português]. 

Codificação

Codificação, também conhecida como “continuização” é a transformação de variáveis categóricas em numéricas (ou binárias). Um exemplo clássico de codificação é gênero: -1,0,1; pode ser usada para descrever masculino, feminino ou outro. Codificação binária é um caso especial onde o valor é ajustado para 0 e 1 para indicar falta ou presença de uma categoria. Codificação “one hot” é outro caso especial, onde múltiplas categorias são cada uma decodificadas binariamente de maneira individual [Para mais detalhes, confira este texto em português sobre o assunto]. Dado um número x de categorias, isso criará x extras características (portanto aumentando a dimensionalidade dos dados [considere aqui cada dimensão como uma variável ou coluna na tabela, por exemplo]). Outro método para decodificar é determinar um alvo e fazer a codificação com base em probabilidade. A categoria é o valor da média e inclui probabilidade.