Se você tem algum bicho de estimação em casa, já deve ter passado por uma situação semelhante. Ao ouvir o som do recipiente com sua comida, o animal prontamente se apresenta.

Em um famoso experimento no início do século XX, o russo Ivan Pavlov explorou isso a fundo. Ele tocava um pequeno sino sempre que ia alimentar um grupo de caẽs e, depois de um tempo, percebeu que os animais começavam a salivar só de ouvir o barulho da sineta. 

De tanto serem submetidos ao estímulo sonoro antes de comer, os cães de Pavlov identificaram uma correlação entre os dois eventos. Toda vez que o sino tocava, a comida era fornecida, então, definitivamente, uma coisa parecia estar fortemente relacionada a outra. E, no experimento, de fato estava.

Mas isso não quer dizer que uma coisa cause a outra. Obviamente, tocar o sino não causa o aparecimento de um prato de comida. 

Sim, estamos no quinto parágrafo do texto e já é chegada a hora de repetirmos um dos adágios mais famosos da estatísticas e ciência de dados. Você provavelmente já estava esperando por ele. Se não, ainda deve ouví-lo muitas vezes em seus estudos: correlação não é causalidade. 

Ou seja, o fato do barulho do sino estar relacionado ao aparecimento da comida não quer dizer que o primeiro cause o segundo. 

Então, tudo bem, correlação não é causalidade. Mas o que é, afinal? 

Neste tutorial, vamos nos debruçar sobre estes dois conceitos, assuntos tão onipresentes quanto propensos a confusões. O tema foi o mais votado na última enquete realizada em nosso programa de membresia.

O que é correlação?

No tutorial ‘Análise com estatística descritiva para leigos’, apresentamos algumas das formas mais básicas de análise de dados, tratando das medidas de tendência central (média, mediana e moda) e medidas de dispersão (desvio padrão e variação interquartil). Em comum a todas elas, está o fato de lidarem apenas com uma variável. 

Mas aqui será diferente. Nós vamos tratar da relação entre duas variáveis.

Vamos começar com um exemplo simples. Imagine que você vai colocar seu imóvel à venda e faz um levantamento do valor das casas na sua rua para definir o valor. 

Então, você toma nota do preço e da área de cada uma.

casa	metros_quadrados	preco
A	40	224,00
B	60	336,00
C	100	560,00
D	250	1.400,00

 

Agora, vamos ver estes números em um gráfico de dispersão (scatterplot). Esta é uma forma muito comum de representar visualmente duas variáveis, quando tratamos do estudo de correlações. 

No gráfico, cada uma das variáveis (no caso, metros quadrados VS preços em milhares) será representada por um eixo (horizontal e vertical, respectivamente). Cada um dos registros será um ponto e sua posição em relação aos eixos será determinada pelos valores de cada variável.

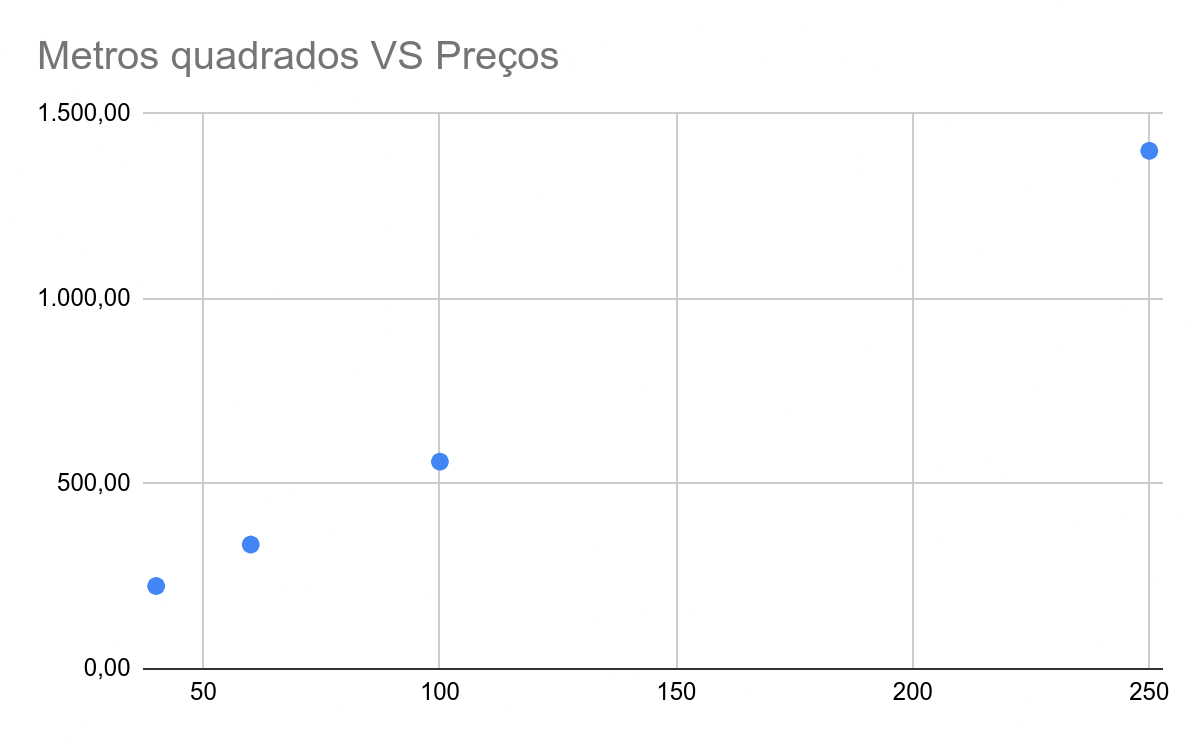
Variável dependente e independente

As variáveis podem ter 3 tipos de interações entre si. A correlação entre elas pode ser: positiva, negativa ou neutra.

Tipo	Descrição	Exemplos comuns
Positiva	Quando o valor de uma variável aumenta, o outro também sobe.	Altura das pessoas VS o tamanho do sapato Tempo de viagem de um avião VS distância percorrida
Neutra	Não há relação entre as duas variáveis.	Consumo de manga por pessoa VS notas em matemática. Altura das pessoas VS quantidade de habitantes de uma cidade.
Negativa	Quando o valor de uma variável sobe, o outro desce.	Distância percorrida VS tempo até a chegada. Refeições feitas em casa VS dinheiro gasto em restaurantes.

 

Além disso, podemos classificar cada variável como dependente ou independente. No primeiro caso, são aquelas que são influenciadas por alguma modificação na outra variável. 

Seguindo o exemplo acima, se você alterar o valor da sua casa, isso mudaria a área dela automaticamente? Não parece razoável, certo? A área não depende do preço, mas o inverso faz sentido. Se a área da sua casa aumentar por alguma razão, o preço dela tende a subir também. Logo, neste caso o preço é a variável dependente.

Já a variável independente, como o nome não indica, não é afetada pela outra variável. No caso acima, a área da casa é a variável independente. Outro exemplo comum de uma variável independente é o tempo ou a idade de alguém.

Em geral, nos gráficos, as variáveis dependentes são representadas no eixo vertical (Y) e as independentes como o eixo horizontal (X).

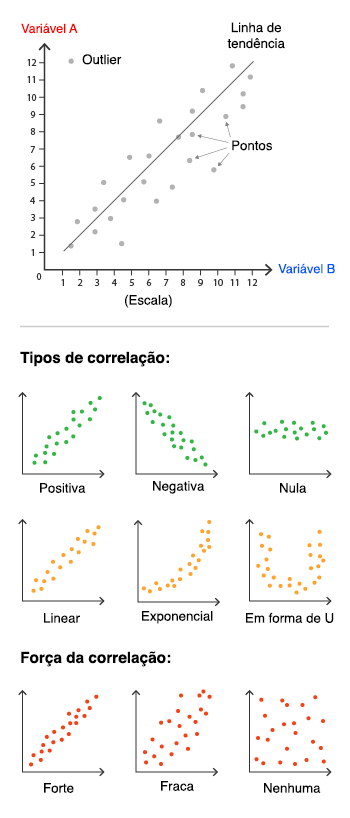
Alguns dos diferentes tipos de correlações possíveis em forma de gráfico. Pareceu confuso? Continua com a gente, pois vamos explicar o que eles significam!

Correlações lineares

Quando há uma correlação entre as variáveis, seja ela positiva ou não, temos ainda um outro tipo de classificação, que nos ajuda a entender como este relacionamento ocorre. 

Antes de adentrar nos conceitos, porém, vamos retomar o gráfico acima. Se você conectar os pontos, vai perceber que irá se formar uma linha reta ascendente.

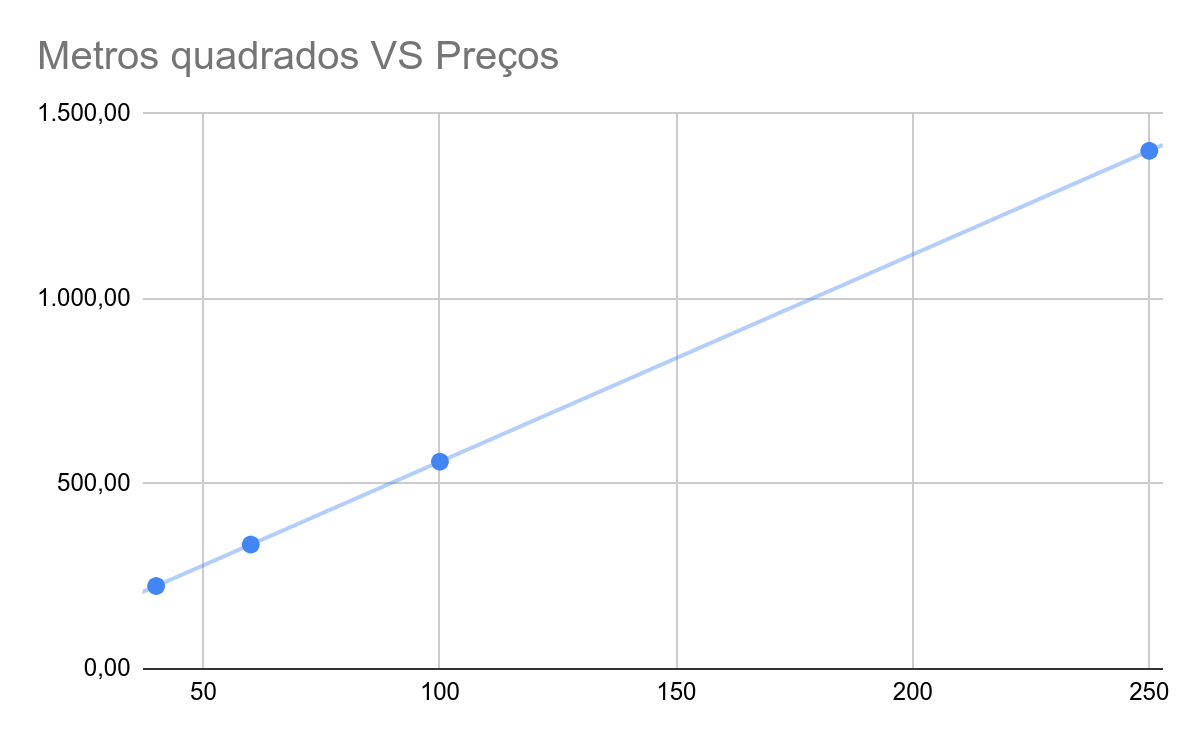
Chamamos essa reta que se forma ao conectar os pontos de “linha de tendência”.

Acima vemos um exemplo de uma correlação linear. Isso significa que a taxa de mudança das variáveis é constante. Em nosso exemplo, todas as casas são avaliadas em R$ 5,6 por metro quadrado. Este valor constante para “traduzir” a área do imóvel em preço faz com que todos os pontos do gráficos fiquem na mesma linha.

Se você quiser aprofundar sua intuição sobre o que significa linearidade na matemática, recomendamos o vídeo ‘Transformações lineares e matrizes’ da excelente série ‘A essência da Álgebra Linear’ do canal 3Blue1Brown. O vídeo tem legendas em português disponíveis.

No “mundo real”, porém, os pontos do seu gráfico de dispersão não ficarão exatamente em cima da linha, tal como no exemplo acima. É possível que exista uma diferença entre a posição do ponto e onde a linha de tendência passa.

Por outro lado, pode ser que a taxa de mudança entre as duas variáveis não seja constante. Por exemplo, se o nosso gráfico for como este abaixo, então seria impossível traçar uma linha reta que se aproximasse de todos os pontos do gráfico. O resultado seria próximo de uma linha curvilínea. Neste caso, teríamos correlação não linear.

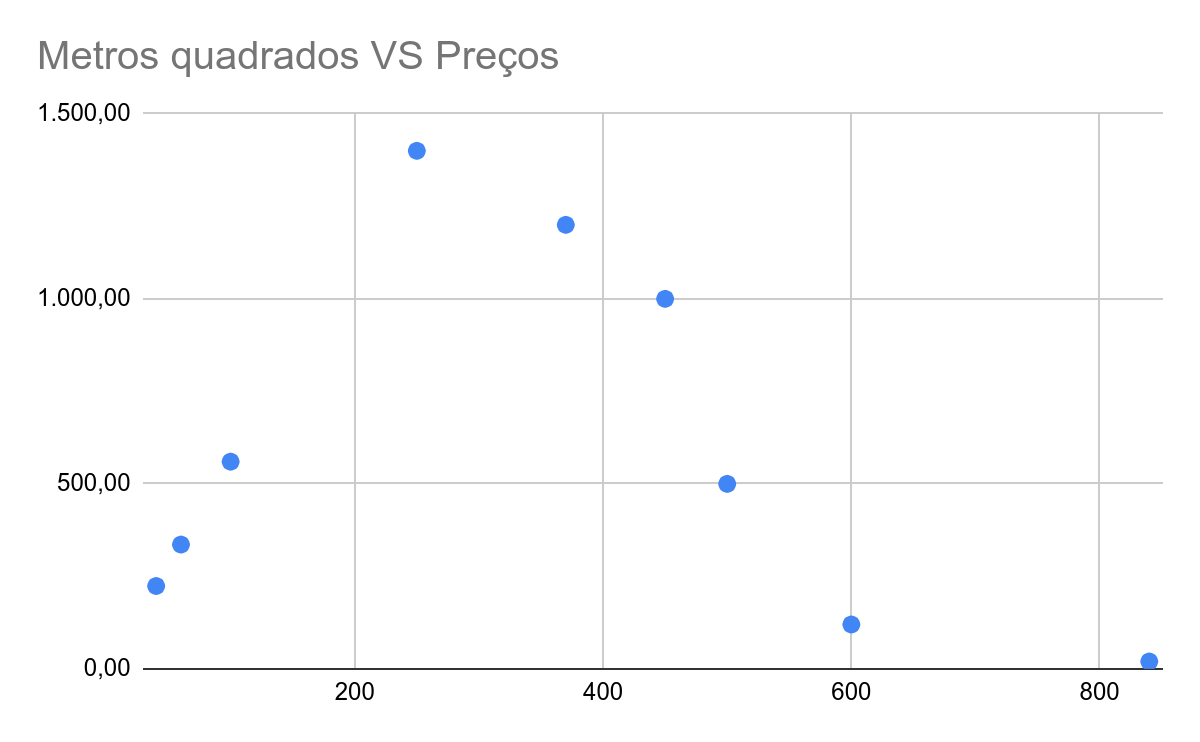
Outro exemplo de correlação não linear pode ser a idade e a altura de uma pessoa. No início da vida, quando a idade aumenta, a altura aumenta, mas só até certo ponto, quando então ela se estabiliza.

Neste tutorial, vamos nos focar nas correlações lineares. Agora que já falamos de algumas classificações gerais sobre correlação, vejamos como mensurá-la.

Coeficiente de relação

Uma correlação linear pode ser medida estatisticamente usando o chamado coeficiente de correlação de Pearson (ou r de Pearson), nome em homenagem ao autor, o cientista britânico Karl Pearson. Usando-o, é possível indicar a força e o tipo de correlação entre duas variáveis com apenas um número. 

O ‘r de Pearson’ será sempre um número entre -1 e 1. Se for zero, então, não há correlação linear entre as variáveis. Mas atenção: é possível que exista uma correlação não linear.

Se for exatamente 1, então, temos uma correlação linear positiva perfeita, como no caso do primeiro gráfico deste tutorial. Por outro lado, se o valor for igual -1 , temos o inverso: uma correlação linear negativa perfeita.

Portanto, se nosso valor for abaixo de zero, temos uma correlação negativa e, quanto mais próximo de -1, mais forte esta correlação negativa será. E, se o número é positivo, então a correlação também será positiva e tanto mais forte quanto mais próxima de 1.

Uma vez que é muito difícil lidarmos com correlações perfeitas, você encontrará diversos valores de referência, para auxiliar na interpretação deste coeficiente de correlação. Estas categorias podem variar de acordo com o referencial adotado ou o campo de estudo, mas veja abaixo uma referência de valores bastante utilizada.

Valor do R de Pearson

Entre 0 – 0.2 Correlação muito fraca

Entre 0.2 – 0.4 Fraca

Entre 0.4 – 0.6 Moderada

Entre 0.6 – 0.8 Forte

Entre 0.8 – 1.0 Muito forte

A correlação não possui unidade de medida. Ou seja, se você mudar a unidade de medida das variáveis, a correlação não muda. Por exemplo, alterar a unidade de medida de Fahrenheit para Celsius não afetará a correlação da temperatura com outras variáveis.

Como calcular o R de Pearson?

Se você quiser se aprofundar na fórmula do coeficiente de Pearson, então, é fundamental se familiarizar antes com os conceitos de desvio padrão e covariância. Existem também algumas diferenças no cálculo, a depender se seus dados são amostrais ou não. Consulte as páginas ‘coeficiente de correlação amostral’ e ‘coeficiente de correlação populacional’ na Wiki Ciência, para mais informações.

Entretanto, felizmente, em geral, você não precisará calcular a fórmula, por conta própria. Podemos usar nossos computadores para fazer isso. 

Abaixo, vamos mostrar três modos diferentes de calcular a correlação entre duas variáveis.

Calculando correlação em editores de planilha

Os editores de planilha possuem uma função que permite calcular a correlação entre duas séries de números. No Google Sheets, isso é feito por meio da função CORREL. A função necessita de dois intervalos de dados (por exemplo, duas colunas) como parâmetros, para poder retornar o R de Pearson.

A fórmula =CORREL(A2:A100;B2:B100) calcula a correlação dos dados listados entre a célula A2 e A100 e aqueles entre B2 e B100.

Veja um exemplo de uso abaixo:

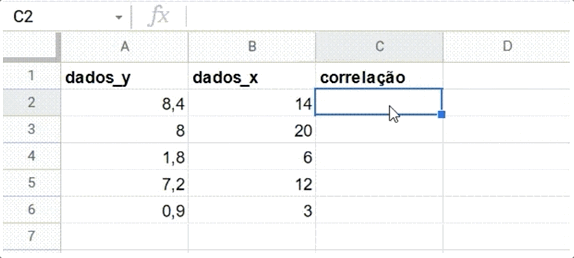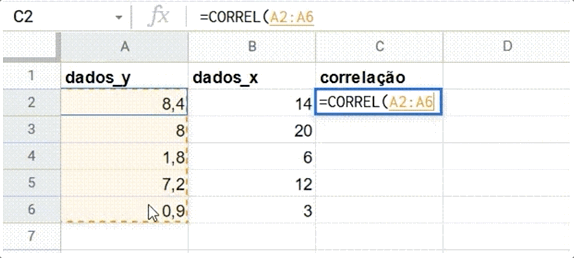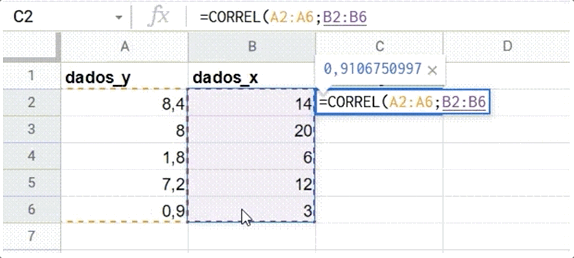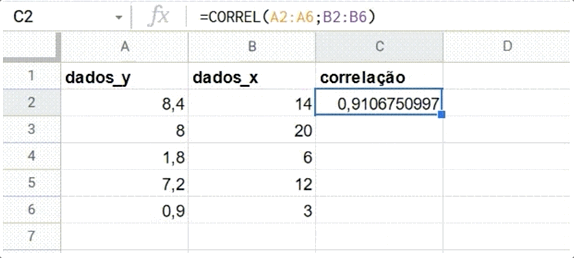
Confira o exemplo do GIF acima nesta tabela do Google Sheets

Correlação em Python e R

Também é possível calcular a correlação usando linguagens de programação, como Python e R.

No primeiro caso, as bibliotecas Scipy, NumPy e Pandas possuem métodos rápidos, abrangentes e bem documentados para essa finalidade.

O scipy.stats contém alguns métodos para calcular coeficientes de correlação e o pearsonr( ) é um deles.

Observe que ele retorna dois valores: o coeficiente de correlação e o valor de p. Você usa o valor de p para testar hipóteses, mas esse é assunto para outro texto. Aqui, estamos interessados apenas no primeiro valor.

A biblioteca Pandas em alguns casos é mais conveniente do que o Numpy e o Scipy para cálculos estatísticos, por oferecer métodos estatísticos tanto para tabelas (dataframe) quanto para colunas (series). No Pandas, o método usado será .corr( ). Para usá-lo você chama uma das variáveis (no nosso caso no X) e passa a outro como argumento para a função (no nosso caso o Y).

Veja o exemplo acima e um caso de uso com dados reais em ação neste notebook.

Em R, existe uma função nativa da linguagem, que permite encontrar o coeficiente de correlação sem a necessidade de recorrer a bibliotecas externas. Basta usar o método cor( ) e então passar as duas variáveis de interesse separadas por vírgula.

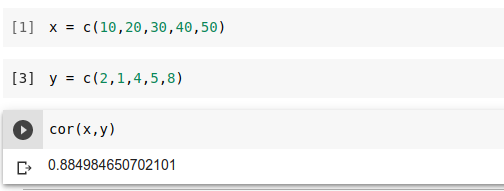
Veja o exemplo acima e um caso de uso com dados reais em ação neste notebook.

Causalidade e variáveis de confusão

Você já viu que verificar a correlação entre duas variáveis é algo trivial de ser feito com um computador. Porém, o mesmo não se aplica para estabelecer uma causalidade entre elas.

Ao investigar qualquer tema em detalhes, provavelmente você irá encontrar correlações. Por exemplo, ao lidar com dados do Censo Escolar, imagine que você descubra uma correlação forte entre a ausência de esgoto nas escolas e a nota do Enem.

Poderíamos dizer que “Se a escola tem esgoto, a nota do Enem é em média X pontos mais alta”? Quer dizer que basta instalar coleta de esgoto nas escolas para as notas aumentarem prontamente? Obviamente não.

As duas coisas podem até estarem correlacionadas, mas estabelecer causalidade entre ambas é algo bem mais complexo.

Ou seja, a correlação nos diz a força e direção do relacionamento entre variáveis, mas nada esclarece sobre os motivos desse relacionamento. Já os estudos sobre causalidade conseguem dar um passo além, indicando que a mudança em uma variável causará uma mudança em outra. Estamos falando aqui das famosas relações de causa e efeito.

Uma relação de causa e efeito acontece quando uma mudança em X causa uma mudança em Y. Em outras palavras, a mudança em Y não está apenas associada a uma mudança em X, ela é diretamente causada por X.

No caso do exemplo anterior, mencionado em uma das aulas de nosso curso ‘Jornalismo de dados para coberturas locais’, de fato, as escolas que não possuem esgoto possuem notas mais baixas, mas existem outros fatores (sociais, econômicos, etc) que impactam tanto a performance dos alunos, quanto a presença ou não de esgoto nas escolas.

Esse mal entendido pode acontecer por termos variáveis “ocultas”, que não foram consideradas na análise, mas influenciam ambas. Estas variáveis são chamadas de variáveis de confusão ou cofounders. Se não forem bem interpretadas, elas podem levar a conclusões inúteis, sugerindo que há causalidade onde não há. 

Existem vários exemplos de “falsas causalidades”, conhecidos como relações espúrias. Um caso famoso é a relação entre países com mais ganhadores do prêmio Nobel e o consumo de chocolate. A pesquisa indicava que o fato do chocolate ter propriedades que melhoram as funções cognitivas possibilitaria países com mais consumidores de chocolate terem mais ganhadores de prêmios Nobel. 

Obviamente, o consumo de chocolate não é suficiente para se tornar mais inteligente. Acontece que os países que mais consomem chocolates são países ricos, com bons sistemas educacionais e outros fatores, que influenciam a quantidade de pessoas ganhadoras do Nobel naquele local.

O estudante de direito, Tyler Vigen, explorou várias bases de dados completamente não relacionados para encontrar conexões inesperadas. Você pode encontrar várias no site Spurious Correlations e no livro do autor.

“Para que a correlação e causalidade seja realizada de forma responsável, é preciso discutir os riscos que possam impedir a causalidade. Testar sua análise é o melhor caminho para isso. Portanto, teste a plausividade destas alternativas. Ter um gráfico bonito não significa que você sabe o que fazer com ele” 

Jonathan Philips no workshop “Interpretando Dados: Se correlação não é causalidade, o que é?” (Coda.Br 2019)

Comunicadores e pesquisadores são responsáveis por pensar como o leitor irá interpretar dados correlacionados. É importante lembrar as limitações dos dados, falando não só das conclusões que podemos extrair a partir deles, mas também aquelas que não podemos deduzir. E, se for o caso, nunca é demais lembrar a sua audiência que correlação não significa causalidade.

Para saber mais Statistics (Robert Pisani, David Freedman) Um dos livros mais recomendados no estudo de estatística. Aborda os principais assuntos com uma narrativa simples. Statistics (John S. Witte e Robert S. Witte) Traz um conteúdo mais denso sobre estatística, indicado para quem quer um aprofundamento maior no assunto. Introduction to Statistics & Data Analysis (Roxy Peck, Chris Olsen, Jay L. Devore) Embora seja um livro introdutório, é uma boa opção para quem quer estudar o assunto aplicando a análise de dados usando linguagem de programação.

 

* O tutorial foi escrito por Adriano Belisario e Anicely Santos, com colaboração do texto de Gabriela Silva de Carvalho, responsável pela cobertura colaborativa do workshop “Interpretando dados: Se correlação não é causalidade, o que é?” realizado por Jonathan Philips no Coda.Br 2019.