Dados: como classificá-los?

*Texto de José Ferraz Neto, originalmente publicado no site O eu analítico.

A grande maioria dos mapas temáticos faz uso de algum método para classificação de dados. O objetivo desse processo é organizar os dados em intervalos de dados ou em classes. A classificação se torna necessária para evitar um nível de granularidade muito elevado tornando a informação incompreensiva. Por outro lado, como apresentado em How to lie with maps um agrupamento incorreto pode distorcer a informação. Atualmente, existem programas (QGIS, ArcGIS, GeoPandas, etc.) que automatizam a produção de mapas com várias configurações default para “facilitar” a vida do usuário. Todavia, tais facilidades podem esconder armadilhas para usuários menos experientes.

Dados podem ser facilmente distorcidos quando analistas sucumbem ao senso de seguir as sugestões padrão das soluções de software. Por exemplo, a maior parte das vezes que um software gera um mapa coroplético a classificação utilizada nos dados é realizada por uma segmentação em 5 categorias baseada em intervalos iguais ou por quantis. (Livre Tradução) Lying with Maps, Mark Monmonier, Statistical Science, 2005, Vol. 20, No. 3, 215–222

Em termos técnicos, o objetivo da classificação de dados é distribuir um conjunto de dados em N categorias, de modo a minimizar a variância dentro dos grupos e maximizá-la entre os grupos. Por exemplo, considere o conjunto de dados a seguir, que representa leituras fictícias de pH.

Iniciamos o processo com a determinação do número de classes (N) e com a escolha do método de categorização. A definição de N está associado a pergunta: O quanto de generalização você deseja em seus dados? Quanto maior for N menor será a generalização associada aos dados, todavia, muitas classes poderão implicar em problemas de legibilidade. Dessa forma, o recomendado é algo em torno de 3 a 7 classes. De sorte que, como regra de ouro, um bom início é avaliar o uso de 5 classes. Quanto ao método iremos utilizar o de intervalo iguais. Assim, calculamos a amplitude (A), para pH temos uma escala adimensional entre 0 e 14, portanto, A = 14. Para calcular o intervalo intra classe: A/N=2.8. Assim, concluímos a definição da distribuição dos dados em diferentes intervalos.

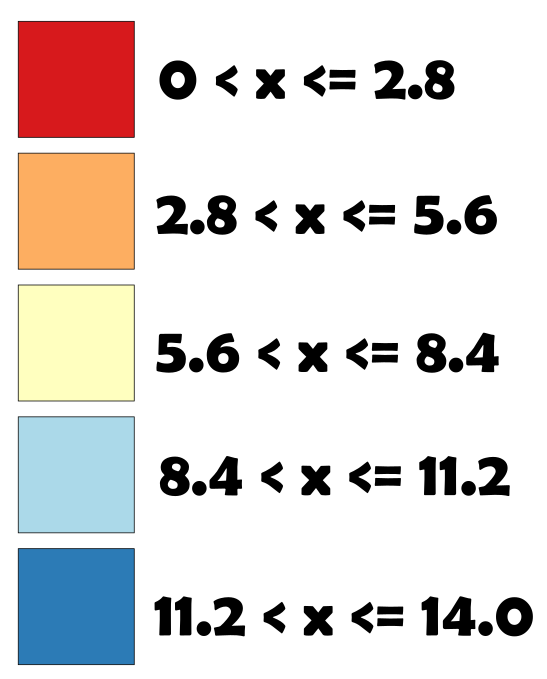
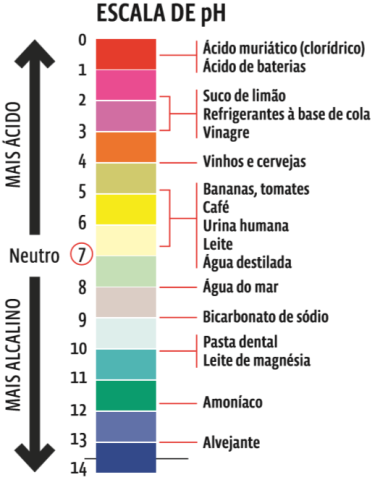
Uma das características desse método é a criação de classes com tamanho iguais. Todavia, quase sempre haverá uma distribuição desbalanceada dos dados nas diferentes categorias, podendo ocorrer alguma distorção por viés amostral em alguma classe, por exemplo. Por outro lado, a decisão de como realizar essa estratificação dos dados pode levar em conta o contexto da análise. O pH é uma medida utilizada em diversas áreas profissionais para mensurar o quão alcalino ou ácido um determinado meio é, como bem apresenta a ilustração abaixo do Guia do Estudante.

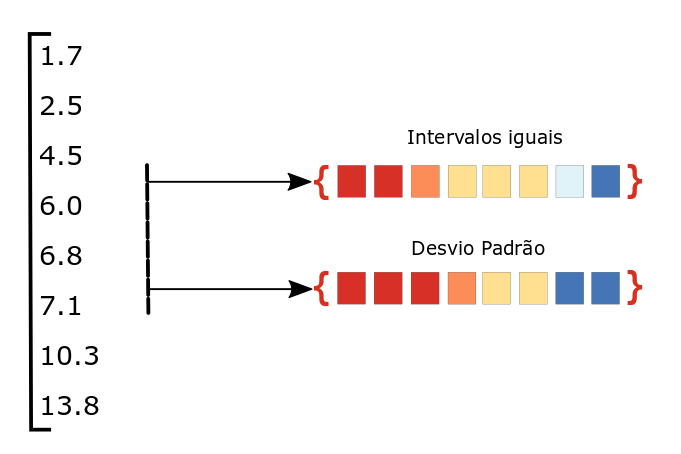
Vamos imaginar que você trabalhe em um órgão ambiental estadual que deve controlar o pH da água do mar das praias de uma cidade. É sabido que a água do mar é levemente alcalina, com pH entre 7,4 a 8,5. Além disso, vamos supor que a série histórica apresente uma média de 7.5 ± 1.2. Uma categorização pode ser efetuada usando-se uma medida de tendência central em conjunto com uma medida de dispersão, como a média e o desvio-padrão (DP), respectivamente. Dessa forma, criamos intervalos contextualizados aos dados. De modo que seja possível avaliar se as leituras de pH estão coerentes com o target, isto é, a média da série histórica.

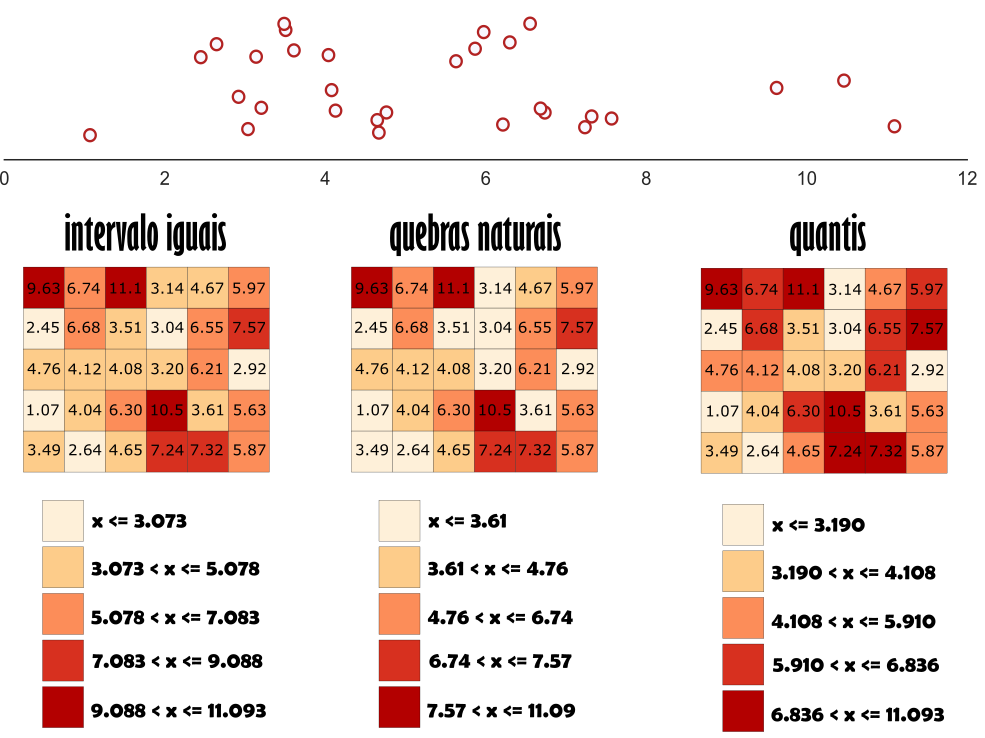
A escolha do método de classificação influenciará o trabalho do analista. Ao ponto que histórias distintas podem ser contadas a partir de um mesmo conjunto de dados. Por exemplo, na figura abaixo são mostradas as escalas de cores produzidas por dois métodos distintos. Assim, são nítidas as mudanças de classificação. Portanto, histórias diferentes podem ser contadas a partir dessas escolhas.

Havendo uma compreensão inicial do que são métodos de classificação de dados e o seu objetivo, podemos explorar com maiores detalhes as principais abordagens existentes. Dessa forma, é válido ressaltar que não há uma única maneira de determinar um número de classes ideal e tampouco um melhor método. Assim, o caminho mais seguro é conhecer os prós e contras de cada abordagem e verificar se ela é apropriada ao seu conjunto de dados em particular.

Achou que iria ser molezinha? Eu também! Mas vamos lá, que não é tão complicado quanto pode parecer. Nesse post, vamos detalhar 4 dos classificadores mais utilizados:

Intervalos iguais (Equal Interval)
Quebras naturais (Natural Breaks)
Quantis (Quantiles)
Customizado (User Defined)

A Análise Exploratória de Dados (AED), disseminada pelo cientista John Tukey, permanece importante nos dias atuais. Várias das técnicas propostas, a serem realizadas durante o processo de AED, nos auxiliarão na tomada de decisão de qual método de classificação é mais apropriado para os seus dados. Para uma melhor compreensão do tópico, convoquei dois personagens que irão me auxiliar a melhor apresentar o assunto. São eles: Seu Creysson e Bino. Os dois atuarão como facilitadores de aprendizagem, em que o Seu Creysson sempre fará os apontamentos que são considerados corretos, enquanto o Bino se encarregará de indicar onde estão as ciladas.

1. intervalos iguais (equal interval)

Como mencionado, serão nossos aliados a AED, a compreensão da distribuição dos dados – por meio de histogramas e de outras visualizações – e o entedimento do assunto estudado.

O método de intervalos iguais realiza uma divisão em classes com intervalos de mesmo tamanho, sendo mais apropriado a dados que se distribuam de forma semelhante por toda a amplitude do dataset. A seguir, temos como exemplo a categorização de um conjunto de dados arbitrário, que possui uma amplitude 100 unidades. Efetuamos a divisão do conjunto em 5 classes, com 20 unidades associadas a cada classe.

O conhecimento sobre as mais diversas distribuições de probabilidade será um aliado importante na tomada de decisão de como classificar os dados. O método de intervalos iguais se apresenta como uma boa opção para dados que se apresentem como uma distribuição uniforme. Todavia, se os dados apresentarem assimetria em alguma das direções ou sejam detectados pontos extremos (outliers), pode ser que alguma categoria fique vazia. Para melhor exemplificar esse conceito, utilizei as bibliotecas Numpy – para gerar dados amostrados de diferentes distribuições- e a PySAL – para avaliar diferentes classificadores.

Ao gerar dois datasets, o primeiro a partir de uma distribuição uniforme e outro a partir de uma distribuição log-normal, foi realizado uma classificação por intervalos iguais com 5 classes. A figura abaixo, com auxílio dos nossos facilitadores de aprendizagem, ilustra bem os exemplos de casos adequados e inadequados de uso desse tipo de classificador. No histograma da esquerda, temos um padrão de dados bem distribuídos em torno de toda a amplitude, configurando o caso ideal de uso desse tipo de classificador. Ao contrário, no da direita, temos uma distriuição com uma assimetria positiva, concentrando a maior parte dos valores na primeira classe, além do fato de que uma das classes ficou sem nenhum valor associado.

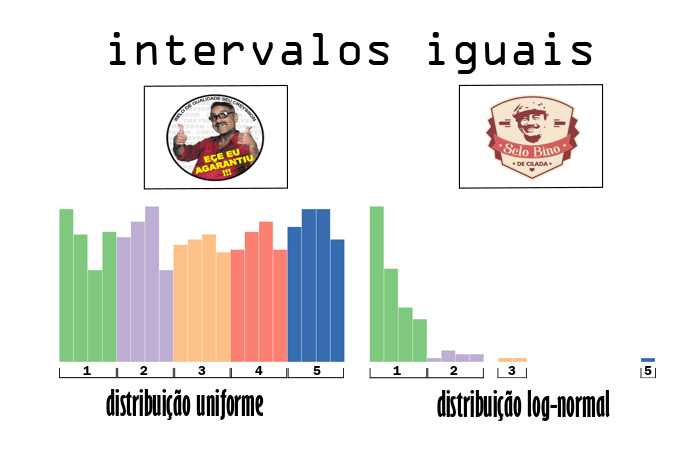
Como vantagem desse tipo de classificação, temos legendas que são mais fáceis de interpretar para audiências não técnicas. No tocante à desvantagem, para dados com distribuições não uniformes, poderão haver agrupamentos desproporcionais em apenas uma ou duas classes.

2. quebras naturais (natural breaks)

Esse método também é conhecido por Jenks – em homenagem ao inventor George Frederick Jenks – e se utiliza de um algoritmo para minimizar a variação em cada grupo. Assim, quando a informação for apresentada em um mapa, as cores tenderão a aparecer mais distribuídas ao longo de toda visualização. O processo de otimização passa por uma iteração em que o algoritmo busca uma minimização da variância dentro dos grupos (agrupando os semelhantes), e maximizando as diferenças entre os grupos (separando os distintos). Além disso, as fronteiras de delimitação das classes são demarcadas nas descontinuidades da distribuição de dados. Portanto, esse método é indicado para ser utilizado em distribuições não normais e não uniformes. A seguir podemos listar algumas características desse método:

vantagens

Mapear valores que não são igualmente distribuídos ao longo da distribuição, resultando em classes mais balanceadas;
As classes geradas possuem o máximo possível de homogeniedade interna;

desvantagens

O mapeamento em classes é inerente ao conjunto de dados em análise, portanto, há uma dificuldade em comparar mapas relacionados a datasets distintos;
Os resultados são bons apenas se existirem descontinuidades na distribuição de dados;

Para representar o que foi explicado acima, foi utilizado o NumPy para criar um amostra de 1000 valores oriundos de uma distribuição binomial. Por conseguinte, foi realizada a classificação utilizando os métodos de quebras naturais e intervalos iguais com 5 classes. A ilustração abaixo apresenta o resultado desse comparativo, onde é possível atestar que a distribuição binomial apresenta algumas descontinuidades. Essa característica configura um dos requisitos de eficácia para o sucesso do algoritmo Jenks. Como resultado, é possível constatar uma distribuição mais homogênea dos valores entre as 5 classes no histograma da esquerda quando comparado ao da direita.

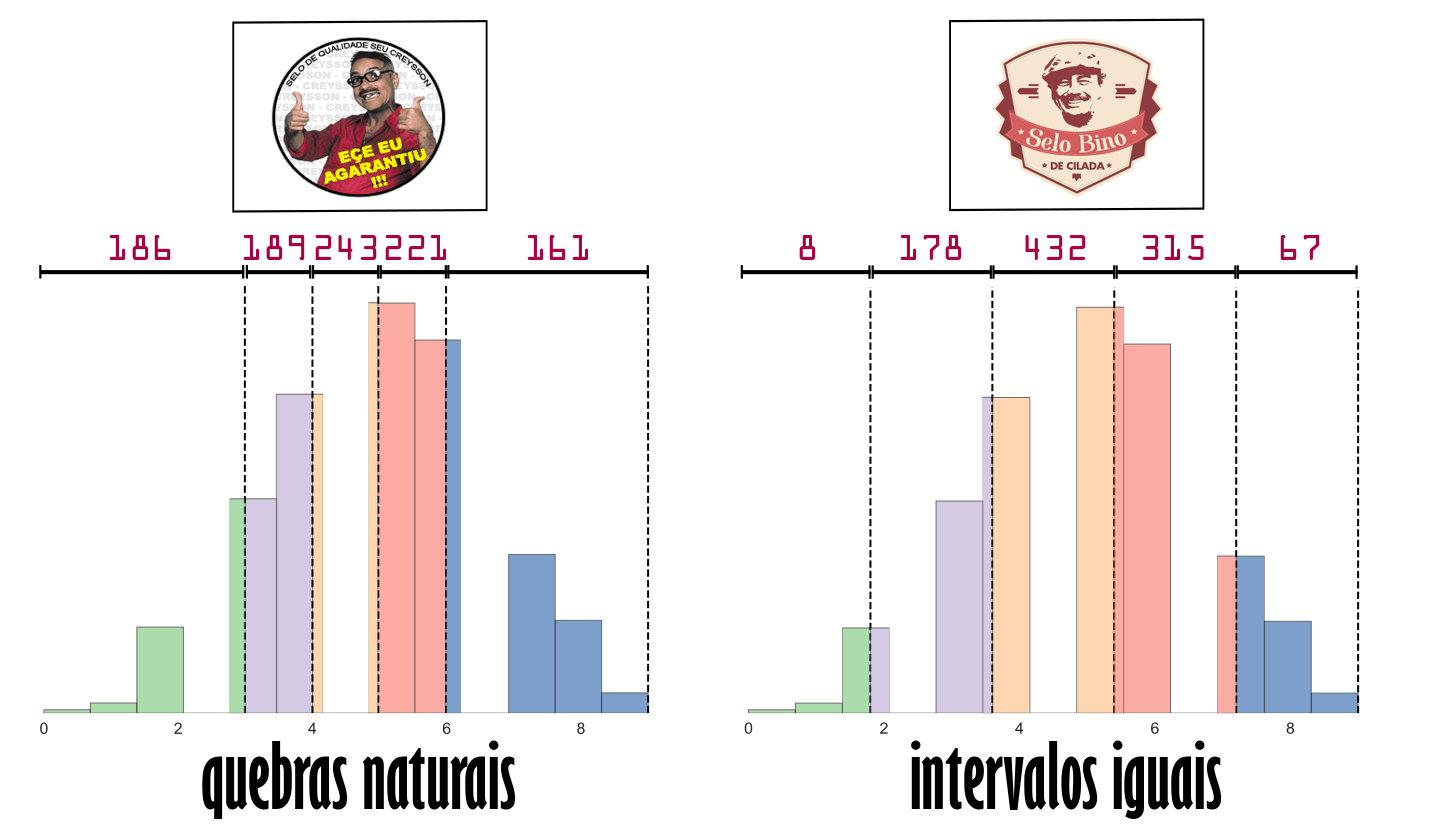
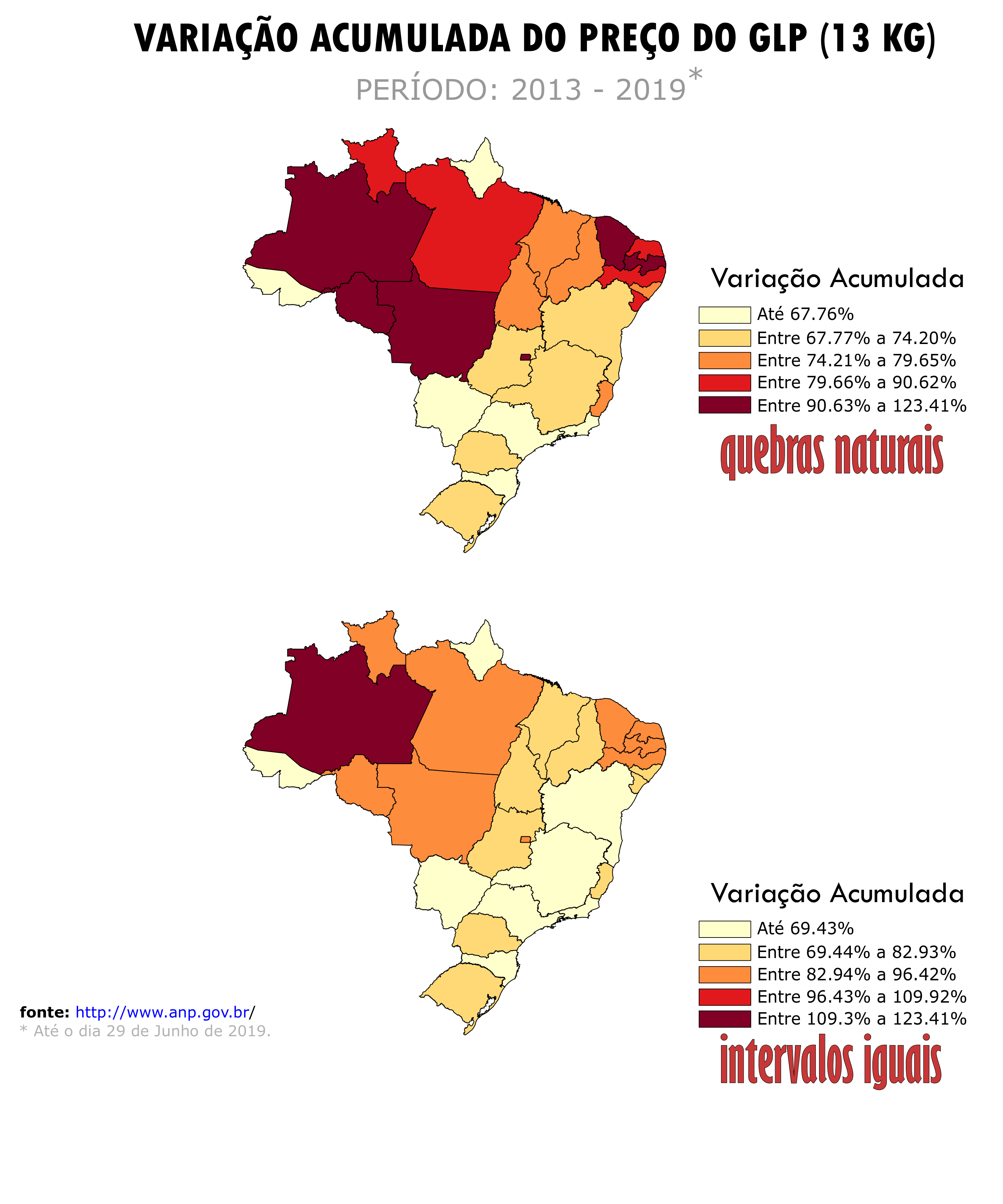
Os histogramas acima apresentam as diferenças entre os métodos comparados. Todavia, o impacto dessa classificação para dados apresentados em um mapa é ainda mais relevante. Considere o Levantamento de Preços e de Margens de Comercialização de Combustíveis realizado pela Agência Nacional do Petróleo, Gás Natural e Biocombustíveis (ANP). Os mapas abaixo apresentam a variação acumulada do preço do gás de cozinha (GLP) – em base nominal – entre janeiro de 2013 a junho de 2019. Logo, quando os dados são classificados pelo método de quebras naturais temos um maior número de estados associados as duas últimas categorias. Assim, evidencia-se que estados do Norte e Nordeste tiveram aumentos percentuais maiores que as demais regiões do país.

3. quantis (quantiles)

A classificação por quantis tenta alocar um mesmo número de observações por classe. Portanto, conjuntos de dados que estão distribuídos de forma homogênea ao longo de toda a distribuição se beneficiam desse tipo de abordagem. A seguir listamos algumas características desse método:

vantagens

É possível enfatizar as posições relativas a determinados valores. Por exemplo, quais observações pertencem aos 20% maiores valores do conjunto de dados?

desvantagens

Valores que pertecem a uma mesma classe podem ser muito diferentes, particularmente, se os dados não estão distribuídos de forma homogênea ao longo da amplitude;
O contrário também pode acontecer, que é o caso de observações muitos próximas serem atribuídas a classes distintas.

Para contornar as desvantagens relatadas acima, uma possível abordagem é alterar o número de classes. De modo a apresentar o uso desse método, foi gerada uma amostra com 1000 observações oriundas de uma distribuição rayleigh, alocando esses dados em 5 classes distintas, uma pelo método dos quantis e outra por intervalos iguais. A ilustração abaixo apresenta a comparação. Como esperado, o primeiro método distribuiu 200 observações por classe, enquanto o segundo concentra 67% dos valores em apenas duas categorias.

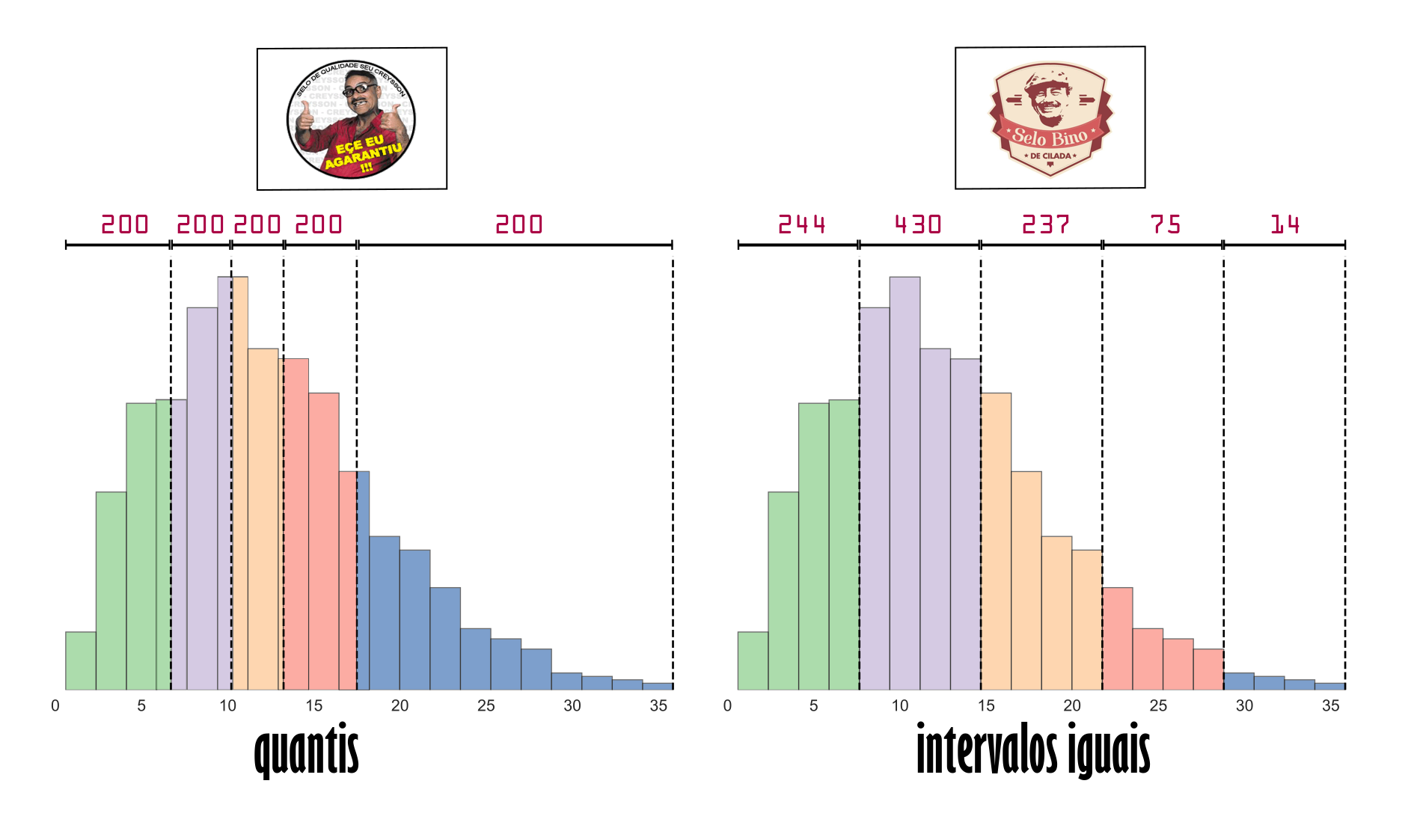
É importante realçar a diferença de abordagem desses dois métodos. A por quantis se propõe a alocar uma mesma quantidade de observações por classe, independentemente da amplitude dessas. Enquanto a segunda preza pelo estabelecimento de classes com intervalos de mesma grandeza, sem ter o compromisso com o quantitativo de observações vinculadas a cada uma delas. De fato, esse método pode gerar classes sem nenhuma observação vinculada.

A importância de realizar uma AED de modo a definir a melhor estratégia de classificação é apresentada a seguir. Usamos os dados do censo de 2010 para construir um mapa coroplético da população por município do estado de São Paulo.

A ilustração abaixo resume os processos realizados até o momento de plotar o mapa. A primeira etapa [a] consiste na construção de um strip plot para avaliar a distribuição ao longo de toda amplitude. Além disso, é possível constatar que os dados se espalham por mais de sete ordens de grandeza, onde a maior parte deles formam uma nuvem de sobreposições no início da escala. Nesse domínio, destacam-se municípios muito populosos, como o caso de São Paulo.

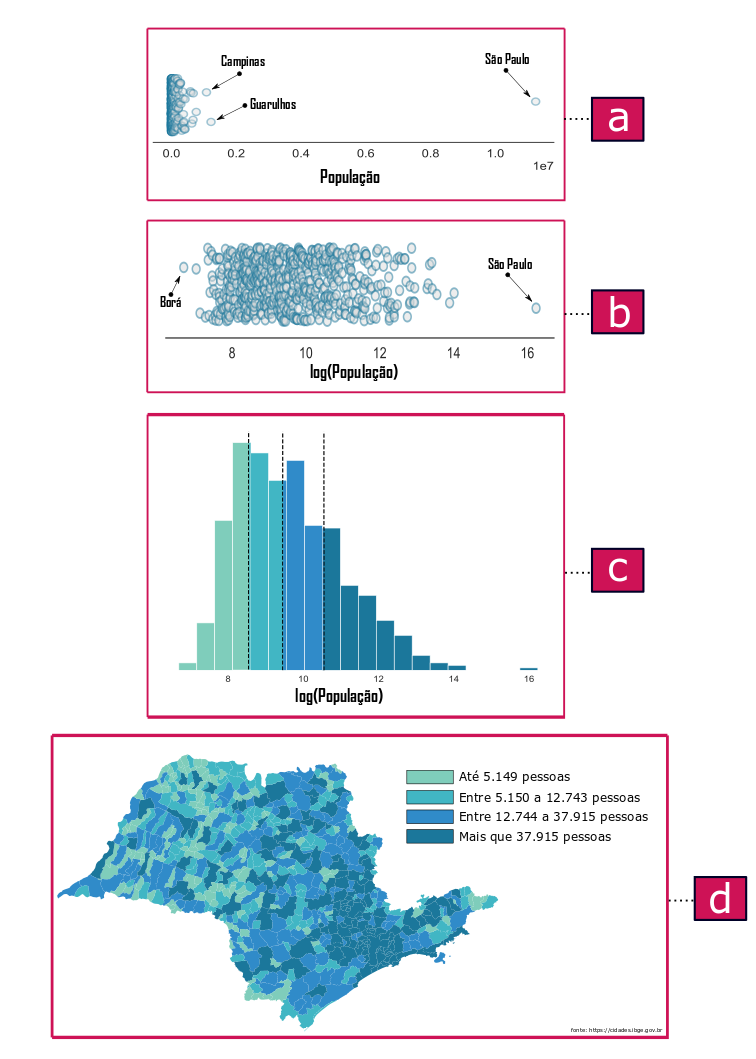
Uma abordagem para analisar dados que possuem outliers extremos como os apresentados no gráfico [a] é fazer uma transformação para uma outra escala, por exemplo, a logarítmica. O gráfico [b] apresenta o resultado dessa transformação. Desse modo, a distribuição dos dados fica mais evidente, tornando possível identificar o município de Borá que possui o menor número de habitantes registrado naquele censo, com apenas 805 habitantes. Diante disso, foi possível aplicar um método de classificação, como o por quantis, como bem ilustra o histograma do gráfico [c]. Por fim, foi possível construir o mapa coroplético [d] com os municípios associados a intervalos populacionais mais adequados.

Demonstramos, até aqui, a importância da escolha adequada de um método de classificação para uma melhor apresentação dos dados. No caso da produção de mapas, os padrões espaciais apresentados serão dependentes do classificador utilizado. Portanto, padrões que existam em um determinado mapa poderão não existir em outro que tenha usado um classificador diferente. Para melhor compreender essas diferenças, observem a ilustração abaixo, que apresenta o uso de diferentes classificadores para um mesmo conjunto de dados. Assim, é possível constatar a diferença nos padrões de mapeamento quando são utilizadas técnicas diferentes.

4. customizado (user defined)

Lembram que mencionei que o conhecimento da regra de negócio associada aos dados é importante? Pois bem: e se o analista julgar que nenhuma das abordagens tradicionais se aplica ao conjunto de dados em análise? Nesse momento, entrará em campo a expertise de negócio, tanto para customizar as fronteiras entre as classes, quanto para definir a melhor forma de distribuir os dados em intervalos customizados. Portanto, faça uso de todas as suas habilidades como analista e explore diversas técnicas – em seu cinto de utilidades de cientista de dados – para uma tomada de decisão mais assertiva.

Assim como proposto, apresentamos 4 abordagens de como classificar dados para construir melhores mapas. Além disso, esse post não esgota todas as opções de classificadores, mas acredito que consiste numa boa introdução a quem deseja compreender as nuances envolvidas na apresentação de dados espaciais. Àqueles que desejam procurar uma fonte de informação para aprofundar seus conhecimentos, indico o livro Designing Better Maps da autora Cynthia Brewer, a mesma que criou a excelente ferramenta Color Brewer.

Por fim, mas não menos importante, gostaria de agradecer aos meu amigos Roberto Mourão, Paulo Haddad, Fernando Barbalho e Romualdo Alves pelas valiosas contribuições a esse texto. Fica aqui o meu muito-obrigado!

E aí gostou do post? Tem alguma sugestão ou dúvida? Deixe um comentário e até a próxima!